Cal aprendre les taules de multiplicar?
Quina és la millor manera de fer-ho?
Què passa si la criatura no les aprèn? Afecta altres aprenentatges matemàtics?
Cal aprendre a multiplicar? O és millor fer servir la calculadora?
Si sou mestres, mares o pares de nens i nenes de tercer curs d’Educació Primària, esteu a punt de plantejar-vos algunes de les qüestions anteriors.
Som al segle XXI i avui sabem moltes més coses sobre l’aprenentatge de les matemàtiques. També sabem el que ens demana la vida social i professional, que va més enllà de l’aplicació mecànica d’algorismes o tècniques de càlcul.
Per ser competent matemàticament parlant, és molt important la comprensió i la capacitat de gestionar els coneixements que tenim per tal de resoldre les situacions en què ens trobem. Cal que els nostres nens i nenes siguin independents intel·lectualment; podríem dir que han de ser in-in, en lloc de ni-ni.
Molta gent, pares i mares i mestres, creuen que les taules de multiplicar són cosa de memòria, i que recitant-les, cantant-les i repetint-les fins a l’esgotament la cosa ja estarà resolta. Bé, doncs això, com us explicaré ara, és cosa del segle passat.
Cònsol, el ximpanzé educat
Us vull presentar una joguina encantadora que va aparèixer a principis del segle xx (1908), patentada per W. H. Robertson als EUA, que volia ser alhora una joguina i un «mestre».

El «cònsol», el mico educat, és una placa metàl·lica de 14 cm × 15 cm que du impresos una colla de números, a la qual se superposa la figura mòbil d’un mico, amb vestit i corbata de llaç i feta d’acer esmaltat prim. Si es col·loquen els peus del mico de manera que assenyalin dos números a la fila de baix de tot, que va de l’1 al 12, les articulacions de metall fan que els braços i el tors canviïn de posició fins que les mans bressolen un resultat. Així, si posem per cas escollim el 4 i el 9, el producte apareixerà emmarcat a la placa posterior: el 36. Quan movem suaument els peus la resta del cos del cònsol es mou amb la coordinació precisa d’un ballarí. (Podeu veure com està fet i com funciona a través d’aquest enllaç).
La invenció del cònsol coincideix amb l’auge de l’educació pública i el progressisme als Estats Units. Aquesta joguina científica encarna aquestes tendències culturals, i proporciona una manera divertida d’aprendre aritmètica i portar les matemàtiques a la llar i a l’escola.
Què significava llavors que un mico fos educat? Segons els psicòlegs i la cultura popular, significava que es pogués comportar com un humà. El 1909, el psicòleg de Pennsilvània Lightner Witmer va utilitzar proves d’intel·ligència dissenyades per a nens «endarrerits» per posar a prova un ximpanzé que s’anomenava Peter, que participava en espectacles de varietats fent veure que era un mico amb la ment d’una persona, i a qui, en les condicions adequades, se li podia ensenyar a llegir, escriure i parlar.
Sembla que hi va haver molts cònsols, i potser va ser gràcies a aquestes estrelles de varietats que «cònsol» es va convertir en la paraula genèrica per designar un mico o un ximpanzé entrenats.
La idea que un mico faci matemàtiques podia agradar als nens per la seva novetat, però el tema subjacent que el mico s’assembli a l’home hauria estat més significatiu per a la població adulta coneixedora de Darwin. Tant els evolucionistes com els antievolucionistes creien que els nens i els primats compartien moltes característiques psicològiques i de desenvolupament, com la simpatia, la picardia i l’expressió emocional.
La joguina s’usava per memoritzar les taules tot jugant. Cap a finals del segle passat se’n van fer diverses reproduccions, i em confesso encantada d’haver-ne trobat una que guardo com una joia.
Però us vull explicar per què m’encanta aquesta joguina mecànica. Primer, perquè és més divertida que buscar els resultats de les taules en un llistat o en una calculadora, però principalment pel seu «misteriós» triangle de números:

Començant per la dreta, trobem els quadrats de l’1 al 12; a la seva esquerra hi ha els múltiples de 12, i després els d’11, els de 10, els de 9, els de 8… fins als de 4, 3 i 2. Si mirem l’altre costat del triangle primer trobem tot de números consecutius; en segon lloc, parells consecutius, i després, múltiples de 3, de 4, de 5, de 6, de 7, de 8, de 9, de 10, d’11 i de 12.
Què passa si comparem el triangle de números amb la taula de 12 × 12? O, millor, amb mitja taula?
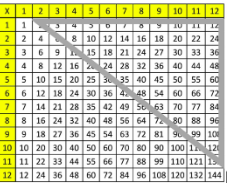
No és el meu propòsit avançar-me a les vostres descobertes, per tant continuo endavant!
Però si em sembla un bon material per descobrir més coses de la multiplicació i divertir-se jugant amb la mona, és perquè les taules de multiplicar s’han d’aprendre entenent el significat de multiplicar. Cada pas s’ha de fer amb comprensió; la memorització pot costar molt i no ser gens productiva a l’hora de fer servir la multiplicació per resoldre situacions.
Una manera de fer comprensiva la multiplicació és representar-la o visualitzar-la en una disposició rectangular com aquestes:
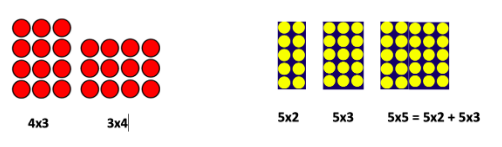
Amb aquests dibuixos la propietat commutativa es fa més entenedora, i també l’associativa i la distributiva. És bo entretenir-se en les primeres taules construint-les amb materials manipulatius, com ara els reglets de la M. Antònia Canals, o dibuixant i retallant paper quadriculat. Després de la taula del 2 es pot fer la del 4, duplicant la del 2; això porta a veure les relacions entre totes dues taules i va configurant interessants relacions multiplicatives entre els nombres. La taula del 6 pot sortir de doblar la del 3 o de triplicar la del 2, etc.
Quan arriba el moment de multiplicar nombres més grans totes aquestes relacions entre els nombres són molt útils i, a més, segur que saben les taules de memòria i les poden visualitzar a ulls clucs.
Els nostres nens i nenes de tercer són capaços de fer matemàtiques, cosa que va molt més lluny d’aprendre regles sense donar-los un sentit.
Per cert, la taula sencera de multiplicar (12 × 12) és digna de ser explorada. Quins són els productes que donen el mateix resultat? Quins són els nombres que es repeteixen més cops a la taula? Per què? I us podeu plantejar moltes altres qüestions.
Sí que us proposo que, si teniu una joguina com la del començament, plantegeu als nens i nenes (a tercer o a quart millor) la comparació entre la taula completa i el triangle de nombres de la joguina.
Si no teniu la joguina podeu usar un interactiu com ara aquest: https://www.edumedia-sciences.com/en/media/24-consul-the-educated-monkey.
I si es fa un bon plantejament de la multiplicació, no hi ha cap problema a cantar les taules! Millor en anglès!
Carme Burgués i Flamarich



